The Limits of Linear Ranking:

This is the third note in a series on quantamental stock rankings. The first note (Ranking Before Prediction), the second one was (Why Learning Factor Weights Is an Ill-Posed Inverse Problem) and the third (Ranking as Selection: From N- grams and Tokens to Equity Universes).
Sorry if this note is a bit heavy on math, but it discusses non obvious things that exclude purely linear methods from a set of instruments able to achieve valid results in stock selection based on rankings.

Consider three stocks, each described by two standardized factors:

Z_PE (cheapness; lower is better)

Z_EPSG (earnings growth; higher is better)
Let their factor vectors be:

Stock A: a = (1, 1)

Stock B: b = (-1, 1)

Stock C: c = (0, 1), Z_PE is zero, means e.g. PE right on sample average, its z-score is zero. But really it is not important.
Assume a linear scoring rule: s(z) = x1 * Z_PE + x2 * Z_EPSG
The scores are:

s(A) = x1 + x2

s(B) = -x1 + x2

s(C) = x2
Notice the identity: s(C) = (s(A) + s(B)) / 2
This holds for all real x1, x2.
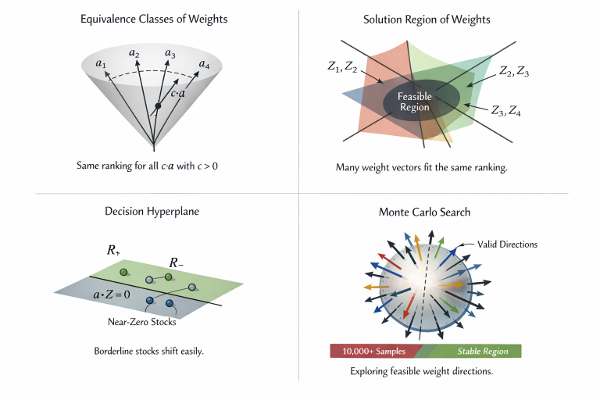
As a result, some orderings are impossible. For example, there is no choice of (x1, x2) such that: s(A) > s(B) > s(C)
This is not a numerical accident. It is a geometric constraint.
This small example captures, in its simplest form, a phenomenon that reappears at scale in real factor models.
Please read the full note 4 in PDF